有限元方法在计算流体力学中的应用
在传统的CFD中广泛使用的方法一般为有限容积法(FVM),基于的是控制容积内积分形式的守恒方程,对整个求解区域进行离散得到整个求解域的方程组。而有限元法则是从变分原理(或加权残值)出发,求使泛函在整个求解域内取极值的节点物理量。有限元法的优点为对于复杂边界有很好的适应性,缺点为对于流体力学的方程中无相应的变分原理,而是直接使用加权残值法处理,求解过程没有明显的物理含义。
1. 流体力学的基本方程组
对于一般不可压缩流体,主要的控制方程为流体的连续性方程和NS(Navier-Stokes )方程
连续性方程
\[ \frac{\partial \rho}{\partial t} + \nabla \rho \boldsymbol{v} = 0\] 动量方程(Navier-Stokes 方程)
\[ \frac{\partial \rho\boldsymbol{v}}{\partial t} + \nabla \cdot \rho\boldsymbol{v} \boldsymbol{v} = -\nabla p + \mu \nabla^2 \boldsymbol{v} + \boldsymbol{f}\] 方程中一共有速度的3个分量和压力4个未知量,并且有4个方程,可以完成求解。
如果流体中涉及能量传递,则需要补充一个能量方程进行温度场的求解;如果流体是可压缩的,则需要补充一个状态方程完成密度场的求解。
2. 流体力学方程组的有限元格式
考虑二维不可压缩流体,使用标准的形函数对待求解的节点速度和节点压力进行插值 \[ \{\boldsymbol{u}\} = [\boldsymbol{N}]\{\boldsymbol{u^e}\} \] \[ \{\boldsymbol{v}\} = [\boldsymbol{N}]\{\boldsymbol{v^e}\} \] \[ \{p\} = [\boldsymbol{N}]\{p^e\} \] 带入到连续性方程和动量方程 \[ \frac{\partial[\boldsymbol{N}]}{\partial x}\{\boldsymbol{u^e}\} + \frac{\partial[\boldsymbol{N}]}{\partial y}\{\boldsymbol{v^e}\} = \{0\}\] \[ [\boldsymbol{N}]\frac{\partial \{\boldsymbol{u^e}\}}{\partial t} + [\boldsymbol{N}]\{\boldsymbol{u^e}\}\frac{\partial[\boldsymbol{N}]}{\partial x}\{\boldsymbol{u^e}\} + [\boldsymbol{N}]\{\boldsymbol{v^e}\}\frac{\partial[\boldsymbol{N}]}{\partial y}\{\boldsymbol{u^e}\} + \frac{1}{\rho}\frac{\partial[\boldsymbol{N}]}{\partial x}\{p^e\} \] \[- \frac{\mu}{\rho}(\frac{\partial^2[\boldsymbol{N}]}{\partial x^2} + \frac{\partial^2[\boldsymbol{N}]}{\partial y^2})\{\boldsymbol{u^e}\} = \{0\}\] \[ [\boldsymbol{N}]\frac{\partial \{\boldsymbol{v^e}\}}{\partial t} + [\boldsymbol{N}]\{\boldsymbol{u^e}\}\frac{\partial[\boldsymbol{N}]}{\partial x}\{\boldsymbol{v^e}\} + [\boldsymbol{N}]\{\boldsymbol{v^e}\}\frac{\partial[\boldsymbol{N}]}{\partial y}\{\boldsymbol{v^e}\} + \frac{1}{\rho}\frac{\partial[\boldsymbol{N}]}{\partial y}\{p^e\} \] \[- \frac{\mu}{\rho}(\frac{\partial^2[\boldsymbol{N}]}{\partial x^2} + \frac{\partial^2[\boldsymbol{N}]}{\partial y^2}) \{\boldsymbol{v^e}\} = \{0\}\] 对以上方程进行加权积分,并进行分布积分,最终得到 \[\iint[\boldsymbol{N}]^T(\frac{\partial[\boldsymbol{N}]}{\partial x}\{\boldsymbol{u^e}\} + \frac{\partial[\boldsymbol{N}]}{\partial y}\{\boldsymbol{v^e}\})dxdy=\{0\}\] \[\iint[\boldsymbol{N}]^T[\boldsymbol{N}]dxdy\frac{\{\boldsymbol{u^e}\}}{\partial t} + \iint[\boldsymbol{N}]^T[\boldsymbol{N}]\{\boldsymbol{u^e}\}\frac{\partial[\boldsymbol{N}]}{\partial x}dxdy\{\boldsymbol{u^e}\}\] \[+\iint[\boldsymbol{N}]^T[\boldsymbol{N}]\{\boldsymbol{v^e}\}\frac{\partial[\boldsymbol{N}]}{\partial y}dxdy\{\boldsymbol{u^e}\} + \frac{1}{\rho}\iint[\boldsymbol{N}]^T\frac{\partial[\boldsymbol{N}]}{\partial x}dxdy\{p\}\] \[+\frac{\mu}{\rho}(\iint\frac{\partial[\boldsymbol{N}]^T}{\partial x}\frac{\partial[\boldsymbol{N}]}{\partial x}dxdy + \iint\frac{\partial[\boldsymbol{N}]^T}{\partial y}\frac{\partial[\boldsymbol{N}]}{\partial y}dxdy)\{\boldsymbol{u^e}\}=\{0\}\] \[\iint[\boldsymbol{N}]^T[\boldsymbol{N}]dxdy\frac{\{\boldsymbol{v^e}\}}{\partial t} + \iint[\boldsymbol{N}]^T[\boldsymbol{N}]\{\boldsymbol{u^e}\}\frac{\partial[\boldsymbol{N}]}{\partial x}dxdy\{\boldsymbol{v^e}\}\] \[+\iint[\boldsymbol{N}]^T[\boldsymbol{N}]\{\boldsymbol{v^e}\}\frac{\partial[\boldsymbol{N}]}{\partial y}dxdy\{\boldsymbol{v^e}\} + \frac{1}{\rho}\iint[\boldsymbol{N}]^T\frac{\partial[\boldsymbol{N}]}{\partial x}dxdy\{p\}\] \[+\frac{\mu}{\rho}(\iint\frac{\partial[\boldsymbol{N}]^T}{\partial x}\frac{\partial[\boldsymbol{N}]}{\partial x}dxdy + \iint\frac{\partial[\boldsymbol{N}]^T}{\partial y}\frac{\partial[\boldsymbol{N}]}{\partial y}dxdy)\{\boldsymbol{v^e}\}=\{0\}\] 从而得到最终的方程组 \[\begin{bmatrix} \boldsymbol{m_{11}} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & \boldsymbol{m_{33}} \end{bmatrix} \frac{\partial}{\partial t} \begin{bmatrix} \boldsymbol{u^e} \\ p \\ \boldsymbol{v^e}\end{bmatrix} + \begin{bmatrix} \boldsymbol{k_{11}} & \boldsymbol{k_{12}} & 0 \\ \boldsymbol{k_{21}} & 0 & \boldsymbol{k_{23}} \\ 0 & \boldsymbol{k_{32}} & \boldsymbol{k_{33}} \end{bmatrix} \begin{bmatrix} \boldsymbol{u^e} \\ p \\ \boldsymbol{v^e}\end{bmatrix} = \{0\}\] 将其记为 \[[\boldsymbol{M}]\{\dot{\boldsymbol{\Phi}}\}+[\boldsymbol{K}]\{\boldsymbol{\Phi}\}=\{0\}\] 对时间采用中心差分格式 \[[\boldsymbol{M}]\frac{\boldsymbol{\Phi_{2}}-\boldsymbol{\Phi_{1}}}{\Delta t} + [\boldsymbol{K}]\frac{\boldsymbol{\Phi_{1} + \Phi_{2}}}{2}=\{0\}\] 得到最终的方程组 \[([\boldsymbol{M}]+\frac{[\boldsymbol{K}]}{2}\Delta t)\{\boldsymbol{\Phi_{2}}\}=([\boldsymbol{M}]-\frac{[\boldsymbol{K}]}{2}\Delta t)\{\boldsymbol{\Phi_{1}}\}\] 即每进行一个时间步长求解需要求解一次以上的方程组。
3. 有限元程序
有限元程序分别为单元部分和求解器,其中单元部分与弹性力学类似只是更换了形函数的计算过程,求解器为标准的有限元求解器只是更改了自由度编号的规则(弹性力学为按照节点排列自由度,这里把相同的自由度排在一起),编程语言使用Julia。
单元部分的核心代码为生成单元刚度矩阵,利用OO特性相关的逻辑并不依赖于单元的具体形式,可使用于任何二维单元,其代码如下
function getStiffMatrix(self::Element2D) ndof = getDofNum(self); nnode = getNodeNum(self); Ke = zeros(Float64, ndof, ndof); nu = self.property.nu; rho = self.property.rho; #对于每一个高斯点进行数值积分 for p in self.points #形函数导数矩阵(局部坐标系) Der = getDerMatrix(self, p); N = getShapeMatrix(self, p); Nx = zeros(1, nnode); Ny = zeros(1, nnode); u0 = 0.0; v0 = 0.0; #计算高斯点上的速度 for i = 1 : nnode node = self.nodes[i]; u0 += node.vals[U::Dof] * N[1, i]; v0 += node.vals[V::Dof] * N[1, i]; i += 1; end #计算形函数矩阵的导数 for i = 1 : nnode Nx[1, i] = Der[1, i]; Ny[1, i] = Der[2, i]; end J = getJacobi(self, p); k1 = 1; k2 = nnode + 1; k3 = nnode * 2 + 1; k4 = nnode * 3 + 1; #积分变换系数和权值 w = abs(det(J)) * last(p); Ke[k1 : k2 - 1, k1 : k2 - 1] += (N' * u0 * Nx + N' * v0 * Ny + nu * Nx' * Nx + nu * Ny' * Ny) * w; Ke[k1 : k2 - 1, k2 : k3 - 1] += (N' * Nx / rho) * w; Ke[k2 : k3 - 1, k1 : k2 - 1] += (N' * Nx) * w; Ke[k2 : k3 - 1, k3 : k4 - 1] += (N' * Ny) * w; Ke[k3 : k4 - 1, k2 : k3 - 1] += (N' * Ny / rho) * w; Ke[k3 : k4 - 1, k3 : k4 - 1] += (N' * u0 * Nx + N' * v0 * Ny + nu * Nx' * Nx + nu * Ny' * Ny) * w; end return Ke; end求解器部分的核心代码为进行一个时间步长的求解,与标准的有限元求解过程基本一致
function solve(self::Model, dt::Float64) ndof = getDofNum(self); nnode = getNodeNum(self); K = zeros(Float64, ndof, ndof); M = zeros(Float64, ndof, ndof); R = zeros(Float64, ndof, 1); inode::Int32 = 1; mnode::Dict{Node, Int32} = Dict{Node, Int32}(); #建立节点到节点编号的映射表 for node in self.nodes mnode[node] = inode; R[inode] = node.vals[U::Dof]; R[inode + nnode] = node.vals[P::Dof]; R[inode + nnode * 2] = node.vals[V::Dof]; inode += 1; end for element in self.elements minode::Dict{Int32, Int32} = Dict{Int32, Int32}(); einode::Int32 = 1; ennode = length(element.nodes); #建立单元的节点自由度编号与总体节点自由度编号映射表 for node in element.nodes inode = mnode[node]; for dofn = 1 : getDofNum(node) minode[einode + (dofn - 1) * ennode] = inode + (dofn - 1) * nnode; end einode += 1; end #总体刚度和质量矩阵的集成(使用得到的自由度编号映射) Ke = getStiffMatrix(element); Me = getMassMatrix(element); (m, n) = size(Ke); for i = 1 : m mi = minode[i]; for j = 1 : n mj = minode[j]; K[mi, mj] += Ke[i, j]; M[mi, mj] += Me[i, j]; end end end #计算最终的刚度矩阵和载荷向量 R = (M - K * dt / 2) * R; K = (M + K * dt / 2); #施加约束 for constraint in self.constraints for node in constraint.nodes inode = mnode[node]; dofn::Int32 = 1; for d in instances(Dof) if haskey(constraint.values, d) idof = inode + (dofn - 1) * nnode; #对对角元增加罚函数 K[idof, idof] += 1e20; R[idof] = constraint.values[d] * K[idof, idof]; end dofn += 1; end end end #进行方程组的求解 self.result = K \ R; #更新节点上的数值 inode = 1; for node in self.nodes node.vals[U::Dof] = self.result[inode]; node.vals[P::Dof] = self.result[inode + nnode]; node.vals[V::Dof] = self.result[inode + nnode * 2]; inode += 1; end end
4. 圆柱绕流问题求解
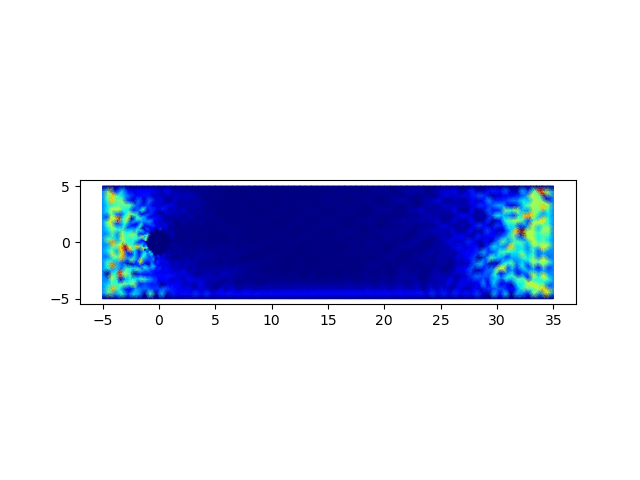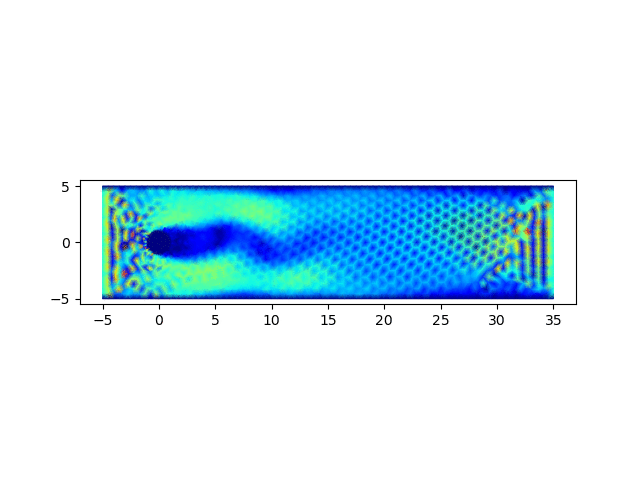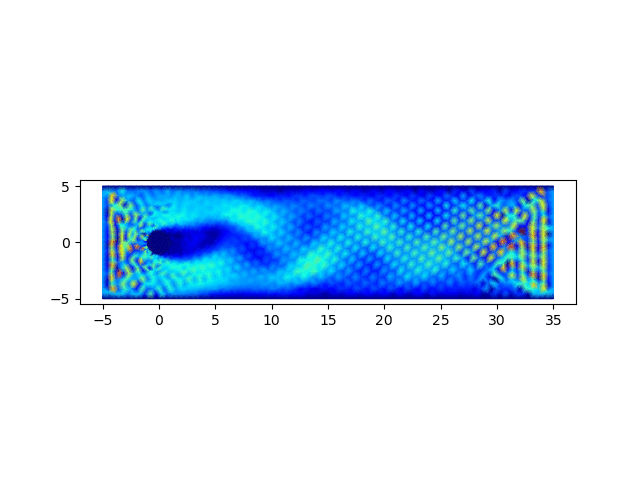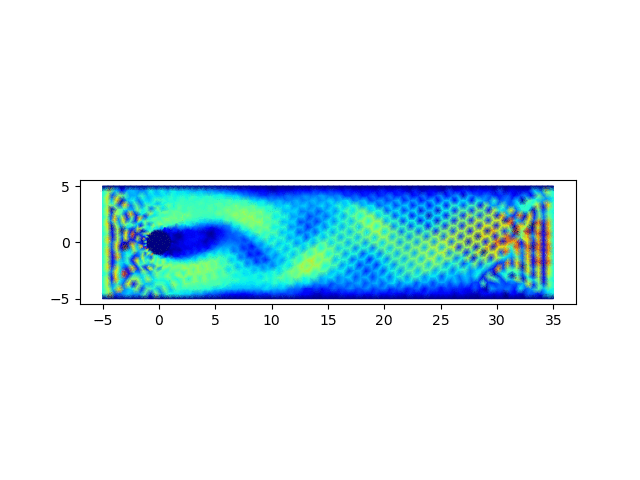
圆柱绕流问题为流体力学中的经典问题,用以上完成的程序进行求解,可以验证程序的正确性
(1) 前处理
虽然Patran作为前处理软件来说并不优秀,但由于对BDF文件格式较为熟悉,故还是选择了Patran。通过几何建模得到一个带有圆孔的长方形区域,并生成三角形网格。对长方形区域的4个边界和圆孔的边界分别设置边界条件(具体边界条件的设置并不重要,主要是为了可以在生成的BDF文件中找到对应边界上的节点)。
虽然不需要用到Patran中的单元属性,但如果不对单元属性进行设置会无法得到完整的BDF文件,为此需要对单元设置一个随意的单元属性。
在分析中选择只输入分析模型文件,同时由于对BDF文件格式解析上的方便,选择small格式的卡片格式。
对BDF文件进行解析的代码如下
local nodes::Dict{Int32, Node} = Dict{Int32, Node}(); local elements::Array{Array{Int32}} = Array{Array{Int32}}([]); for line in eachline("A9.bdf") if line[1] != '$' local len = length(line); local n = len ÷ 8 + 1; local card = strip(line[1 : 8]); #解析单元和节点 if card == "CTRIA3" local nids::Array{Int32} = Array{Int32}([]); local id = parse(Int32, String(strip(line[9 : 16]))); for nid in split(strip(line[25 : end]), r"\s+") push!(nids, parse(Int32, String(nid))); end push!(elements, nids); elseif card == "GRID" #对数字的科学计数法进行处理,BDF文件中指数为负数时省略了e local x::Float64 = parse(Float64, replace(String(strip(line[25 : 32])), r"\-(\d+)$" => s"e-\1")); local y::Float64 = parse(Float64, replace(String(strip(line[33 : 40])), r"\-(\d+)$" => s"e-\1")); local id = parse(Int32, String(strip(line[9 : 16]))); node = Node(x, y); nodes[id] = node; end end end(2) 边界条件的设定
进口出处的节点设定为恒定速度u = 5,v = 0,上下边界处速度均设定为0,出口处设定为恒定速度u = 5,v = 0保证区域内的质量守恒。相关的代码如下
local spc1 = SPC(); addConstraint(spc1, U::Dof, 5.0); addConstraint(spc1, V::Dof, 0.0); addConstraint(spc1, P::Dof, 0.0); for i = 83 : 101 addNode(spc1, nodes[i]); nodes[i].vals[U::Dof] = 5.0; end for i = 108 : 200 addNode(spc1, nodes[i]); nodes[i].vals[U::Dof] = 5.0; end local spc2 = SPC(); addConstraint(spc2, U::Dof, 0.0); addConstraint(spc2, V::Dof, 0.0); addConstraint(spc2, P::Dof, 0.0); for i = 1 : 82 addNode(spc2, nodes[i]); end for i = 102 : 181 addNode(spc2, nodes[i]); end for i = 201 : 250 addNode(spc2, nodes[i]); end addConstraint(m, spc1); addConstraint(m, spc2);(3) 求解
求解的过程较为简单,只需要安装设定的时间补偿循环一定的次数即可,每步完成后记录相应的结果,为了方便进行后处理,结果保存为3个文件——节点信息文件,单元信息文件,计算结果文件
#通过命令行给定计算的步数 local n = parse(Int32, ARGS[1]); for i = 1 : n solve(m, 0.05); save(m, "data"); end(4) 后处理
由于Julia没有提供比较合适的绘图库(有的一种本质上也为调用的matplotlib),这里使用Python提供的matplotlib进行分析结果的可视化。
计算结果可以绘制流场图和速度云图,绘制流场图的代码如下
import matplotlib.pyplot as plt; x = []; y = []; u = []; v = []; p = []; m = []; for line in open('data.1'): row = line.strip().split(" "); x.append(float(row[0])); y.append(float(row[1])); for line in open('data.2'): row = line.strip().split(" "); u0 = float(row[0]); v0 = float(row[2]); u.append(u0); p.append(float(row[1])); v.append(v0); for line in open('data.3'): row = line.strip().split(" "); m.append([int(row[0]) - 1, int(row[1]) - 1, int(row[2]) - 1]); fig, ax = plt.subplots(); ax.set_aspect('equal'); q = ax.quiver(x, y, u, v); plt.savefig(sys.argv[1] + '.png');从以0.05的时间步长计算400步,生成的结果图中可以观察到,圆柱附近涡的形成、发展和脱落的过程,可参见下面的动图。